虹桥飞机场出租车数据分析报告

从数据我们可以得到五种数据：

label yy1='逗留时间=等待时间+服务时间'; f10

label yy2='排队长度'; fi中非零数据个数

label yy3='服务时间'; 做差fi-f(i-1)

label yy4='服务流量'; 单位时间（一小时）内fi中非零数据个数

label yy5='顾客流量'; 一天内fi中非零数据个数

下面对排队长度数据进行分析。服务流量、顾客流量数据分析类似。

1． 识别性分析：识别原始数据

对原始数据进行原始识别处理，先画柱状图形（直方图）和饼状图形如下

从图形可以猜想，其图形是普松分布。

普松分布的一阶矩估计为

myyy=myy-minyy;

lambda1=myyy ; 3.28571

普松分布的二阶矩估计为

lambda2=ssyy**2; 6.37372

普松分布的区间估计为（见茆诗松和周纪芗，概率论与数理统计，中国统计出版社，2007，p334-337）

lambdaxx=mn*myyy;

array kk[1000] kk1-kk1000;

do k=1 to 1000;

kk[k]=1-poisson(lambdaxx,k)-probchi(2*lambdaxx,2*(k+1));

if k>2 and kk[k]<0 then goto ok;

end;

ok:;

lambdaxx=cinv(0.05, 2*k)/(2*mn); 3.11526

lambdal=cinv(0.025, 2*k)/(2*mn); 3.07970

lambdau=cinv(0.9755, (2*k+1))/(2*(mn)); 3.54494

lambdasx=cinv(0.95, 2*k)/(2*mn); 3.50296

lambdazwqj=cinv(0.5, 2*k)/(2*mn); 3.30532

1． 稳健性分析：比较各种估计的差别

普松分布的一阶矩估计和普松分布的区间估计两种估计比较接近， 但普松分布的二阶矩估计与前两者差别很大。用三种估计的平均值作为参数lambda 的估计应是比较稳健的

lambdaqz=(lambda1+lambda2+lambdazwqj)/3;  4.32159

即使不考虑二阶矩估计，用其他两种估计的平均值作为参数lambd的估计也应是比较稳健的

lambdaqz=(lambda1+lambdazwqj)/2; 3.29552

3． 协调性分析：比较估计分布与经验离散频率分布

3.2：诊断估计分布与经验离散频率分布图形的协调性

以上述参数作为普松分布的估计与经验离散频率分布函数的比较图形为

从图形看出拟合不好.

即使不考虑二阶矩估计，用其他两种估计的平均值作为参数lambd的估计,以此参数作为普松分布的估计与经验离散频率分布函数的比较图形为

从图形看出拟合也不好. 尽管它看起来比前一种好一点，即图形的接近程度高一些, 但两种分布的差别还是较大。

3.2：估计分布与经验离散频率分布理论的协调性

用皮尔逊的Kf统计量进行拟合检验两种情况都没有通过.

N=238, l=1, Kf= 728.110 >  272.836 (显著性水平0.05)

N=238, l=1, Kf= 325.637 >  272.836 (显著性水平0.05)

其中n为数据个数，l为估计参数个数。而Kf 为经验离散频率分布函数和拟合分布的差的平方的加权和， 近视为KF统计量，自由度为

（n-l-1），272.836是统计量Kf显著性水平0.05临界值。

4．功能性分析：变换原始数据

上述分布的各种参数为

mn myy c d ssyy maxyy minyy pz yyp50 mu myyy lambda1 lambda2 lambdaxx k lambdal

238 3.28571 1 0 2.52462 8  0  3 3  0 3.28571 3.28571 6.37372 3.11526 9 3.07970

lambdau lambdasx lambdazwqj lambdaqz xitaz ddd kkk  p  i xitaL xitaU   fun

3.54494 3.50296 3.30532 4.32159 4.32159 1 3 0.89678 8 1.32159 7.32159 平时柏松分布

其中普松分布的一阶矩估计和普松分布的二阶矩估计不一致, 这可能是估计不准确的原因。为了消除这个原因，我们采用数据变换的方法解决。

对数据yy做变换：

myyy=myy-minyy;

c=(myyy)/(ssyy**2); 0.51551

d=0;

yy=int((myyy+d)*c);

（此时变换后的均值为变换前的c倍，而变换后的方差为变换前的c^2倍,令两者相等，得到上述的变换公式，由于取整数函数int(*)有低估现象，可以用d来做小的调整）。

用这些数据进行上述同样的分析得到图形如下

从图形看出效果很好。

用皮尔逊的Kf统计量进行拟合检验通过.

N=238, l=3, Kf= 13.8675 < 270.684  (显著性水平0.05)

其中n为数据个数，l为估计参数个数。而Kf 为经验离散频率分布函数和拟合分布的差的平方的加权和， 近视为KF统计量，自由度为

（n-l-1），270.684是统计量Kf显著性水平0.05临界值。

得到的分布参数为

mn  myy   c  d  ssyy maxyy minyy pz yyp50 mu  myyy lambda1

238 1.35714 0.51551 0 1.19888  4   0  1  1  0 1.35714 1.35714

lambda2 lambdaxx k lambdal lambdau lambdasx lambdazwqj lambdaqz  xitaz

1.43731  1.25542 4 1.23303 1.53415  1.50566  1.37675  1.39040 2.69714

xita

ddd kkk   p   i  L  xitaU    fun     CL   UCL  LCL

1  3  0.94735 6  0  5.69714 平时柏松分布 2.63262 5.75277  0

其中普松分布的一阶矩估计(lambda1 =1.35714)和普松分布的二阶矩估计(lambda2 = 1.43731 )基本一致.这可能就是估计准确的原因。数据变换方法使得两个估计接近相等。

5．经济性分析：变换控制图

根据变换后的估计分布的控制图，变回到原来分布的控制图的控制限为

UCL= 5.75277

CL= 2.63262

LCL=0

要求每五个数据进行平均得到一个点（低于五个数据平均时，由于随机性太强，控制图波动性太大，看不出规律性）。

由此得到控制图为：

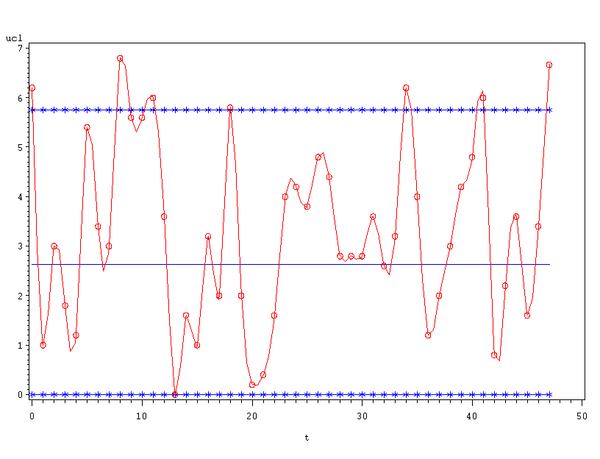
从图中看到：排队长度分布具有高峰期发生，高峰期发生的条件可以判定为队长大于五。用这个条件我们可以分析各种数据的高峰现象。对应的底峰期发生的条件也可以判定为队长不大于六, 用这个条件我们也可以分析各种数据的低峰现象。